„Cel care mută un munte începe întotdeauna prin a îndepărta pietrele mai mici.”
Confucius
Dragul meu părinte bine te-am regăsit! De o săptămână a început școala iar perioada următoare este pentru toți elevi una solicitantă deoarece urmează perioada tezelor. Așa că azi îți propun un model de teză rezolvat și explicat pas cu pas pe înțelesul tuturor, dar și un model nerezolvat (asemănător) pe care copilul tău să îl rezolve singur urmărind modelul rezolvat de mine.
Model Teza clasa a VI-a Semestrul II
Subiectul I (total 4,5 puncte):
Exercițiul 1 (0,5 puncte):
Rezultatul calculului :
......................................
- Rezolvare:
Exercițiul 2 (1 punct):
Termenul necunoscut x din proporția:
este: ...................................
- Rezolvare:
Transformăm fracția zecimală în fracție ordinară.
Exercițiul 3 (1 punct):
din 450 este egal cu: ..........................................
- Rezolvare:
Exercițiul 4 (1 punct):
Dacă
atunci
.....................................
- Rezolvare:
- Dăm factor comun și la numărător și la numitor pe "b".
Înlocuim fracția cu fracția
Aducem la același numitor :
Fracția de la numărător o împărțim la fracția
adică o înmulțim cu răsturnata acestei fracții:
Exercițiul 5 (1punct):
Soluția ecuației
este:................................
- Rezolvare:
Subiectul II: (total 4,5 puncte):Pe foaia de examen se trec rezolvarile complete.
Exercițiul 1 (1,5 puncte):
Rezolvați în Z inecuația:
Rezolvare:
Desfacem paranteza după care separăm termenii cu x într-o parte iar cei fara x în cealaltă parte.
Exercițiul 2 (1,5 puncte):
Rezolvați în Z ecuația:
- Rezolvare:
Exercițiul 3 (1,5 puncte):
Fie triunghiul dreptunghic ABC cu
, având
.
Se construiesc
,
, cu
,
și
. Să se arate:
a)
b)
c)
Rezolvare:
Scriem datele problemei:
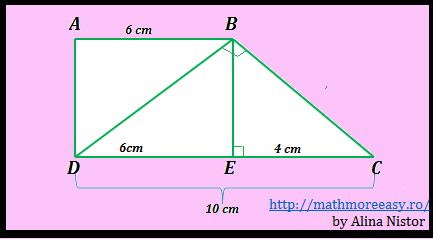
Realizăm desenul respectând datele problemei.

- a)
-
- b)
și
:
și
dar
În avem :
și
(Conform teoremei unghiului de
)
Dar în
și
(Conform teoremei unghiului de
)
Dar mai sus am gasit
c) :
și
:
și
Dragul meu părinte, sper din tot sufletul ca aceste informaţii să îţi fie utile atunci când îţi ajuţi copilul la temele pentru acasă la matematică. Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimite un e-mail la adresa:nistor_madalina2005@yahoo.com
Dacă ai în jurul tău un parinte sau un copil care are dificultăți în a înțelege matematica fă un gest frumos și recomandă-i
Cu mare drag şi mult respect Alina Nistor!








 Încearcă să fii un om de valoare și nu neapărat un om de succes. – Albert Einstein
Încearcă să fii un om de valoare și nu neapărat un om de succes. – Albert Einstein
 Dacă A reprezintă succesul în viață, Atunci A= x+y+z, în care x reprezintă munca, y reprezintă joaca, iar z să știi să-ți ții gura. – Albert Einstein.
Dacă A reprezintă succesul în viață, Atunci A= x+y+z, în care x reprezintă munca, y reprezintă joaca, iar z să știi să-ți ții gura. – Albert Einstein.