puterile lui 2 - Matematica Mai Usoara

Etichetă: puterile lui 2

06
sept.
2017

Exerciții rezolvate la Pătrate Perfecte!

"Nu poți împinge pe nimeni să urce pe o scară dacă nu este dispus să o urce singur "
Andrew Carnegie

Dragul meu părinte bine te-am regăsit! În articolul anterior am prezentat cateva "Exerciții Rezolvate la Ultima Cifră a unui Număr Natural". Astăzi te invit să rezolvăm și să explicăm câteva exerciții la Pătrate Perfecte. Să vedem cum putem arăta că un număr foarte mare poate fi sau nu pătrat perfect!

Exercițiul 1:
Arătați că numărul $a=2003 + 2\cdot (1+2+3+................+ 2002)$ este pătrat perfect.

Rezolvare: Pentru a arăta că numărul "a" este pătrat perfect trebuie să arătam că numărul "a"se poate scrie ca un număr natural la puterea a doua.
Observăm că în paranteză avem Suma Gauss a primelor 2002 numere naturale consecutive așa că vom aplica formula de calcul a lui Gauss.
$a=2003 + 2\cdot (1+2+3+................+ 2002)$
$a=2003 + 2\cdot [2002\cdot (2002+1)\ : \ 2]$
$a=2003 + 2\cdot [2002\cdot 2003 \ : \ 2]$
Pentru că înmulțirea și împărțirea sunt operații de același ordin putem efectua mai întâi operația de împărțire.
$a=2003 + 2\cdot [2002\ \ : \ 2 \cdot 2003]$
$a=2003 + 2\cdot 1001 \cdot 2003$
$a=2003 + 2002 \cdot 2003$
Dăm factor comun pe 2003.
$a=2003\cdot (1 + 2002)$
$a=2003\cdot 2003$
$a=2003^2$ .
$\Rightarrow numarul \$ este pătrat perfect.

Exercițiul 2:
Arătați că numărul $a=81+81 \cdot 2+ 81 \cdot 3+.....................+81 \cdot 49$ este pătrat perfect.

Rezolvare: Pentru a arăta că numărul "a" este pătrat perfect trebuie să arătam că numărul "n"se poate scrie ca un număr natural la puterea a doua.
Observăm că 81 se repetă și îl putem da factor comun.
$a=81\cdot (1+ 2+ 3+.....................+49).$
În paranteză obținem Suma Gauss a primelor 49 numere naturale consecutive așa că vom aplica metoda de calcul a lui Gauss.
$a=81\cdot [49 \cdot(49+1) \ \ : \ 2 ]$
$a=81\cdot [49 \cdot 50 \ \ : \ 2 ]$
$a=81\cdot 49 \cdot 25$
$a=9^2\cdot 7^2 \cdot 5^2$
Aplicăm Regulile de Calcul cu Puteri și obținem:
$a=(9\cdot 7 \cdot 5)^2$
$a=315^2$

Exercițiul 3:
Arătați că numărul $n= 27^9 \cdot 32^{11} \ \ : \ \ 2 - 16^6\cdot 2\cdot 6^{27}$ este pătrat perfect.

Rezolvare: Pentru a arăta că numărul "n" este pătrat perfect trebuie să arătăm că se poate scrie ca un număr natural la puterea a doua.
Observăm că pe 27 îl putem scrie ca bază 3, pe 16 și 32 îi putem scrie ca baza 2 iar pe 6 îl putem scrie ca produsul $2\cdot 3$
$n= (3^3)^9 \cdot (2^5)^{11} \ \ : \ \ 2^1 - (2^4)^6\cdot 2^1 \cdot (2\cdot3)^{27}$
Aplicăm Regulile de calcul cu puteri și obținem:
$n= 3^{3\cdot9} \cdot 2^{5\cdot 11} \ \ : \ \ 2^1 - 2^{4\cdot 6}\cdot 2^1 \cdot 2^{27}\cdot 3^{27}$
$n= 3^{27} \cdot 2^{55} \ \ : \ \ 2^1 - 2^{24}\cdot 2^1 \cdot 2^{27}\cdot 3^{27}$
$n= 3^{27} \cdot 2^{55-1} - 2^{24+1+27}\cdot 3^{27}$
$n= 3^{27} \cdot 2^{54} - 2^{52}\cdot 3^{27}$
$n= 3^{27} \cdot 2^{52} \cdot 2^2 - 2^{52}\cdot 3^{27}$
Observăm că se repetă $3^{27} \cdot 2^{52}$ și îi dăm factor comun.
$n= 3^{27} \cdot 2^{52} \cdot (2^2 - 1)$
$n= 3^{27} \cdot 2^{52} \cdot (4 - 1)$
$n= 3^{27} \cdot 2^{52} \cdot 3$
$n= 3^{27} \cdot 2^{52} \cdot 3^1$
$n= 3^{27+1} \cdot 2^{52}$
$n= 3^{28} \cdot 2^{52}$
$n= (3^{14} \cdot 2^{26} )^2$ $\Rightarrow n$ este pătrat perfect

Exercițiul 4:
Arătați că numărul $n= 2^{2011}- 2^{2010}-2^{2009}-2^{2008}$ este pătrat perfect.

Rezolvare: Pentru a arăta că numărul "n" este pătrat perfect trebuie să arătăm că se poate scrie ca un număr natural la puterea a doua.
Aplicând Regulile de Calcul cu Puteri putem scrie: $2^{2011}= 2^{2008}\cdot 2^{3}$ ; $2^{2010}= 2^{2008}\cdot 2^{2}$ și $2^{2009}= 2^{2008}\cdot 2^{1}$ . Obținem astfel:
$n= 2^{2008}\cdot 2^{3} - 2^{2008}\cdot 2^{2} - 2^{2008}\cdot 2^{1} -2^{2008}$
Observăm că se repetă $2^{2008}$ și putem sa îl dăm factor comun:
$n= 2^{2008}\cdot (2^{3} - 2^{2} - 2^{1} - 1)$
$n= 2^{2008}\cdot (8 - 4 - 2 - 1)$
$n= 2^{2008}\cdot 1$
$n= 2^{2008}$
$n= (2^{1004})^2$ $\Rightarrow n$ este pătrat perfect

Exercițiul 5:
Arătați că numărul $a= 2^{1504} + 2^{1505} + 2^{1506} +..............+ 2^{2002}$ nu este pătrat perfect.

Rezolvare: Observăm că avem Suma Gauss a puterilor lui 2. Pentru a rezolva acest exercițiu înmultim întreaga expresie matematică cu un 2.
$a= 2^{1504} + 2^{1505} + 2^{1506} +..............+ 2^{2002} | \ \ \ \cdot2$
$2\cdot a= 2\cdot 2^{1504} + 2\cdot 2^{1505} + 2\cdot 2^{1506} +..............+2\cdot 2^{2002}$
$2\cdot a= 2^{1504+1} + 2^{1505+1} + 2^{1506+1} +..............+ 2^{2002+1}$
$2\cdot a= 2^{1505} + 2^{1506} + 2^{1507} +.............+2^{2002}+ 2^{2003}$
Scădem cele două relații și obținem:
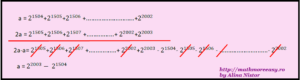
suma gauss a puteror lui 2
$a = 2^{2003} - 2^{1504}$
Pentru a demonstra că numărul $a = 2^{2003} - 2^{1504}$ nu este pătrat perfect trebuie să arătăm că Ultima cifră a lui a aparține mulțimii: $\left \{ 2,3, 7,8 \right \}$ .
Calculăm Ultima cifră a numărului: $a = 2^{2003} - 2^{1504}$
$U(a) = U(2^{2003} - 2^{1504})$
$U(a) = U(2^{2003}) - U(2^{1504})$
Calculăm $U(2^{2003})$ .
Mai întâi calculăm puterilelui 2.
Observăm că ultima cifră se schimbă din 4 în 4.
Împărțim 2003 la 4 și obținem câtul 500 și restul 3.
$U(2^{2003})=U(2^{4\cdot 500+3})=U[(2^4)^{500}\cdot 2^3]=U[(2^4)^{500}]\cdot U(2^3)$
Dacă privim atent puterile lui 2 observăm ca ultima cifră a lui $2^4$ este 6 și astfel obținem:
$U[(2^4)^{500}]\cdot U(2^3)= U[U(6^{500})\cdot 8]$
Știm că 6 ridicat la orice putere are ultima cifra tot 6.
Și obținem: $U[U(6^{500})\cdot 8]=U(6 \cdot 8)= U(48)=8$
Am obținut că $U(2^{2003})=8$
Calculăm $U(2^{1504})$ .
Împărțim 1504 la 4 și obținem câtul 376.
$U(2^{1504})=U(2^{4\cdot 376})=U[(2^4)^{376}]$
$U(2^4)=6$ $\Rightarrow U[(2^4)^{376}]=U(6^{376})=6$
Am obținut astfel: U(a) = U(2^{2003}) - U(2^{1504})=8-6=2
Știm că ultima cifră a unui pătrat perfect nu poate fi 2 $\Rightarrow$ $a= 2^{1504} + 2^{1505} + 2^{1506} +..............+ 2^{2002}$ nu este pătrat perfect.

Succes! PS: Nu uita să te abonezi pentru a afla când postez lectii video și dă un share să afle și prietenii tăi ! Math More Easy - YouTube https:/ https://www.facebook.com/MathMoreEasy. Cu mare drag şi mult respect Alina Nistor

08
aug.
2017

Exerciții rezolvate la Ultima Cifră a unui Număr Natural

categories: Numere Naturale

"Zadarnic vei vrea să-l înveți pe cel ce nu e dornic să fie învățat, dacă nu-l vei fi făcut mai întâi dornic de a învăța."
Comenius

Dragul meu părinte bine te-am regăsit. În articolul anterior am vorbit despre cum putem afla Ultima cifră a unui număr natural. Azi îți propun câteva exemple de exerciții rezolvate și explicate pas cu pas la această lecție dificilă pentru clasa a V-a.

Exercițiul 1:

Calculați ultima cifră a numerelor:

a) $2^{1299}; \ \ \ 2^{2020};$

b) $21^{324}; \ \ \ 19^{257}; \ \ \ 17^{2020};$

Rezolvare:

a) Pentru a calcula $2^{1299};$ mai întâi privim atent puterile numărului 2.

Observăm că ultima cifră se repetă din 4 în 4. Împărțim puterea 1299 la 4 și obținem: $1299 \ \ \ : \ \ \ 4=324 \ \ \ rest \ \ \ 3$ $\Rightarrow 1299=4\cdot 324 +3$ Atunci putem scrie că: $U(2^{1299})=U(2^{4\cdot 324 +3})=U[(2^{4})^{ 324} \cdot 2^3)]$ $=U[(2^{4})^{ 324}] \ \ \ \cdot \ \ \ U( 2^3)$ Consultăm tabelul cu puterile lui 2 și observăm că $2^{4}$ are ultima cifră 6 astfel obținem: $U[(2^{4})^{ 324}] \ \ \ \cdot \ \ \ U( 2^3)=U(6^{ 324}) \ \ \ \cdot \ \ \ 8$ Consultăm tabelul cu puterile lui 6.

Observăm că 6 ridicat la orice putere are ultima cifră 6 astfel obținem: $U(6^{ 324}) \ \ \ \cdot \ \ \ 8=U(6 \cdot 8)=U(48)=8$ Am obținut că $U(2^{ 1299})=8$ Calculăm acum pentru $U(2^{ 2020})=?$ Avem mai sus tabelul cu puterile lui 2 și am observat că ultima cifră se repetă din 4 în 4. Împărțim puterea 2020 la 4 și obținem: $2020 \ \ \ : \ \ \ 4=505 \ \ \ rest \ \ \ 0$ Atunci putem scrie că: $U(2^{2020})=U(2^{4\cdot 505 +0})=U[(2^{4})^{ 505} \cdot 2^0)]$ . Știm că orice număr ridicat la puterea 0 este egal cu 1 $\Rightarrow 2^{0}=1$ . Am văzut mai sus că $2^{4}$ are ultima cifră 6 astfel obținem: $=U[(6^{ 505} \cdot 1)]=U(6 \cdot1)=6$ . Am obținut că: $U(2^{ 2020}) = 6$ b) $21^{324}; \ \ \ 19^{257}; \ \ \ 17^{2020};$

Calculăm $U(21^{ 324}) = ?$

$U(21^{ 324}) = U(1^{ 324})$ Știm că 1 ridicat la orice putere este egal cu 1. $\Rightarrow U(1^{ 324}) = 1$

Calculăm $U(19 ^{ 257}) = ?$

$U(19 ^{ 257}) = U(9^{ 257}) =$ Calculăm puterile lui 9.

Observăm că ultima cifră se repetă din 2 în 2. Împărțim 257 la 2 și obținem: $257 \ \ \ : \ \ \ 2 = 128 \ \ \ rest \ \ \ 1$ Atunci putem scrie că: $U(9^ {257})= U(9^ {2\cdot128+1})= U(9^ {2})^{128} \cdot U(9^1)=$ Consultând tabelul cu puterile lui 9 observăm că $9^2$ are ultima cifră egală cu 1, astfel obținem: $U(9^ {2})^{128} \cdot U(9^1)= U(1^{128})\ \ \ \cdot \ \ \ 9=U(1 \cdot 9 )=9$ Am obținut că $U(19^{ 257}) = 9$

Calculăm $U(17^{ 2020}) = ?$

$U(17^{ 2020}) = U(7^{ 2020})$ = ? Calculăm puterile lui 7.

Observăm că ultima cifră se repetă din 4 în 4. Împărțim 2020 la 4 și obținem: $2020 \ \ \ : \ \ \ 4 = 505 \ \ \ rest \ \ \ 0$ Atunci putem scrie că: $U(7^{ 2020}) = U[(7^4)^{ 505}]$ Consultând tabelul cu puterile lui 7 observăm că $7^4$ are ultima cifră egală cu 1, astfel obținem: $U[(7^4)^{ 505}] = U(1^{505})=1$ Am obținut că $U(17^{ 2020})=1$ .

Învăț pentru mine
Dragul meu părinte își propun câteva exerciții pe care să le rezolve copilul tău urmărind exemplele explicate și rezolvate mai sus! Determină ultima cifră a numerelor: a) $2^{99}; \ \ \ 2^{2018}; \ \ \ 2^{2024};$ b) $41^{2017}; \ \ \ 125^{2017}; \ \ \ 2017^{2018};$ c) $4^{1999}; \ \ \ 129^{2022}; \ \ \ 2016^{2018};$

Succes! PS: Nu uita să te abonezi pentru a afla când postez lectii video și dă un share să afle și prietenii tăi ! Math More Easy - YouTube https:/ https://www.facebook.com/MathMoreEasy. Cu mare drag şi mult respect Alina Nistor

02
aug.
2017

Ultima cifră a unui număr natural

categories: Numere Naturale

"Cu cât un copil a văzut și a înțeles mai mult, cu atât vrea el să vadă și să înțeleagă mai mult."
Jean Piaget

Dragul meu părinte bine te-am regăsit! În articolul anterior am vorbit despre "Pătratul unui număr natural". Astăzi îți propun o nouă lecție care mă ajută să demonstrez dacă un număr natural este pătrat perfect sau nu: "Ultima cifră a unui număr natural".

Șirul de numere: 0, 1, 4, 9, 16, 25, 36, ............... este șirul $0 ^{2}, 1 ^{2}, 2 ^{2}, 3 ^{2}, 4 ^{2}, 5 ^{2}, 6 ^{2}, .............., n ^{2}, ..........$ și se numește șirul numerelor naturale pătrate perfecte. Fie $x$ un număr natural. Notăm cu $U(x)$ ultima cifră a numărului $x$ . Să privim cu atenție următorul tabel:

Observăm ca ultima cifră a unui pătrat perfect poate fi: $0, 1, 4, 5, 6 \ \ sau \ \ \ 9$ . Observație:

Dacă ultima cifră a unui număr natural este $2, 3, 7\ \ sau \ \ \ 8$ atunci acel număr natural nu poate fi pătrat perfect.
Dacă ultima cifră a unui număr natural este $0, 1, 4, 5, 6 \ \ sau \ \ \ 9$ acel număr natural este pătrat perfect.

Pentru a afla ultima cifră a unui număr vor avea în vedere următoarele reguli de calcul:

$U(x+y)=U(U(x)+U(y))$

$U(x\cdot y)=U(U(x)\cdot U(y))$

$U(x^n)=U[(U(x))^n]$

Exemple:

$U(79 +24)=U(U(79) +U(24))=U(9+4)=U(13)=3$

$U(98 \cdot 82)=U(U(98) \cdot U(82))=U(8 \cdot 2)=U(16)=6$

$U(36 ^{89})=U(U(36) ^{89})=U(6^ ^{89})=6$

Să analizăm atent următorul tabel:

Observație:

Numerele $1,5 \ \ \ si \ \ \ 6$ ridicate la orice putere îmi dă ultima cifră $1,5 \ \ \ si \ \ \ respectiv \ \ \ 6$ .

La numerele $2,3, 7 \ \ \ si \ \ \ 8$ se repetă ultima cifră din patru în patru puteri. La aceste numere ca să pot afla ultima cifră împart exponentul la 4, iar ultima cifră va fi egală cu ultima cifră a numărului 2,3,7 sau respectiv 8 ridicat la puterea egală cu restul împărțirii.

Iar la numerele $4 \ \ \ si \ \ \ 9$ se repetă ultima cifră din două în două puteri.La aceste numere ca să pot afla ultima cifră împart exponentul la 2, iar ultima cifră va fi egală cu ultima cifră a numărului 4 sau respectiv 9 ridicat la puterea egală cu restul împărțirii.

Exemple: Determinați ultima cifră a numerelor:

$2^{{2017}}\ \ \ si \ \ 4^{{2017}}$

Rezolvare:

Calculăm pentru $2^{{2017}}$ . Scriem puterile lui 2.

Observăm ca ultima cifră se repetă din 4 în 4. Împărțim 2017 la 4

Obținem astfel $2017\ \ \ : \ \ \ 4 =504 \ \ \ rest \ \ \ 1$ Rezultă că $U(2^{2017})= U[(2^4)^{2017} \cdot 2^1]=U(2^4)^{2017}\cdot U(2^1)$ Privind puterile lui 2 observăm că ultima cifră a lui $2^4$ este 6, iar ultima cifră a lui $2^1$ este 2. Astfel obținem că $U(6^{2017})\cdot 2= U(6 \cdot 2) = U(12) = 2$

Observație: Am precizat mai sus ca 6 la orice putere are ultima cifră egala tot cu 6.

Calculăm ultima cifră pentru numărul $U(4^{2017})$ =

Scriem puterile lui 4.

Observăm că la numărul 4 ultima cifră se repetă din 2 în 2. Împărțim 2017 la 2 :

Obținem astfel: $2017 \ \ \ :\ \ \ 2 = 1008 \ \ \ rest\ \ \ 1$ Rezultă că: $U(4^{2017})=U[(4^2)^{1008} \cdot 4^1]=U[(4^2)^{1008}] \cdot U(4^1)=$ Ultima cifră a lui $4^2$ este 6 iar ultima cifră a lui $4^1$ este 4. Înlocuiesc și obțin: $U(6^{1008})\cdot U(4^1)= U(6 \cdot 4)= U(24)= 4$ . Te invit să exersezi și tu 3 exerciții identice pe care ți le propun în rubrica:

Învăț pentru viitorul meu: Determină ultima cifră a numerelor: $9^{2017}; \ \ \ 3^{2019} ;\ \ \ 8^{2021}.$

Succes! PS: Nu uita să te abonezi pentru a afla când postez lectii video și dă un share să afle și prietenii tăi ! Math More Easy - YouTube https:/ https://www.facebook.com/MathMoreEasy. Cu mare drag şi mult respect Alina Nistor

Etichetă: puterile lui 2

Exercițiul 1:

Exercițiul 2:

Exercițiul 3:

Exercițiul 4:

Exercițiul 5:

Știm că ultima cifră a unui pătrat perfect nu poate fi 2 nu este pătrat perfect.

Învăț pentru mine

Știm că ultima cifră a unui pătrat perfect nu poate fi 2 $\Rightarrow$ $a= 2^{1504} + 2^{1505} + 2^{1506} +..............+ 2^{2002}$ nu este pătrat perfect.