Subiecte rezolvate Evaluare Naţionala 2015

Dragul meu părinte, mai sunt doar 4 zile până la Examenul de evaluare naţională pentru elevii de clasa a VIII-a.

În articolul precedent am rezolvat şi explicat exerciţiile date la Sesiunea Evaluării Naţionale 2015.

În acest articol voi aborda exerciţiile date la Evaluarea naţională sesiunea Specială pentru Olimpici 2015.

Fiecare exerciţiu îl voi rezolva şi explica pas cu pas, menţionând şi punctajul aferent fiecarui exerciţiu conform baremului de corectare, astfel ca ţie să-ţi fie uşor să-i explicit copilului tău cum să rezolve şi să trateze fiecare exerciţiu pentru a obţine un punctaj cât mai mare la examenul de capacitate care va avea loc pe data de 29 iunie 2016.

SUBIECTUL I - Pe foaia de examen scrieţi numai rezultatele.

Rezultatul calculului 20 : 2 -10 este egal cu 0.

Rezolvare: Pentru că avem o operaţie de împărţire şi o operaţie de scădere, facem întâi operaţia de împărţire apoi scăderea si obţinem 10-10=0.

Dacă $\frac{a}{6}=\frac{25}{3}$ , atunci "a" este egal cu ..50.

Rezolvare: Pentru al afla pe “a” facem produsul mezilor egal cu produsul extremilor şi obţinem:

$3 \cdot a=6\cdot25\Rightarrow3a=150 \Rightarrow a=150 \div 3 \Rightarrow a=50.$

Cel mai mic număr natural din intervalul [2,6] este egal cu 2.

Rezolvare:Pentru că avem un interval închis (paranteza este pătrată) putem lua valoarea 2.

Perimetrul unui triunghi echilateral este egal cu 18cm. Lungimea unei laturi a acestui triunghi este egală cu ..6.cm.

Rezolvare: Ştim că perimetrul este suma tuturor laturilor. Dar laturile unui triunghi echilateral sunt egale.

$P=3 \cdot l \Rightarrow 3\cdot l=18 cm \Rightarrow l=18 cm \div 3 \Rightarrow l=6 cm$

În Figura 1 este reprezentat un con circular drept cu raza bazei AO = 3cm şi înălțimea VO = 4cm . Generatoarea VA a acestui con este egală cu ..5..cm.

Rezolvare: Ştim că ∆ VOA este dreptunghic în unghiul O. În acest caz aplicăm teorema lui Pitagora pentru a afla ipotenuza VA.

$\Delta VOA(<O=90^\circ) VA^2=VO^2 + AO^2$

$VA^2=4^2 + 3^2$

$VA^2=16 + 9$

$VA^2=25$

$VA=\sqrt{25}=5$

În tabelul de mai jos sunt prezentate temperaturile măsurate la o stație meteorologică, la aceeași oră, în fiecare zi a unei săptămâni din luna mai.

Cea mai mică temperatură măsurată în acea săptămână a fost de ..12..°C.

Pentru fiecare răspuns correct se acordă 5 puncte.

SUBIECTUL al II-lea - Pe foaia de examen scrieţi rezolvările complete.

Desenaţi, pe foaia de examen, un cub ABCDA'B'C'D

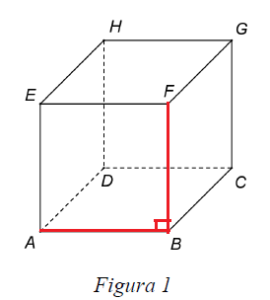
Pentru desenarea corectă a cubului se obţin 4 puncte, iar notarea corectă a cubului se punctează cu 1 punct.

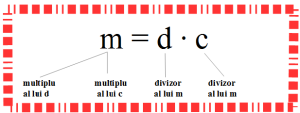
Calculaţi media aritmetică a numerelor naturale care sunt divizori ai lui 7.

Rezolvare: Stim din clasa a V-a că numărul natural „b” divide numărul natural „a”, dacă există numărul natural „c”, astfel încât a = b · c.

Dragul meu părinte găseşti mai multe informaţii despre “Divizor. Multiplu” aici: http://mathmoreeasy.ro/divizor-multiplu/ .

Dar să revenim la exerciţiul nostru şi să vedem care sunt divizorii numărului 7.

$D_{7}=\left \{ 1;7 \right \}$

$M_{{a}}=\frac{a+b}{{2}}=\frac{1+7}{{2}}=\frac{8}{{2}}=4$

Pentru scrierea formulei mediei aritmetice şi identificarea celor 2 divizori se acordă 3 puncte, iar obţinerea rezultatului corect al exercitiului se punctează cu 2 puncte.

Numerele x şi y sunt direct proporţionale cu numerele 3 și 4 . Determinați cele două numere, ştiind că y este cu 14 mai mare decât x.

Rezolvare : Am învăţat în clasa a VI-a Mărimi direct proporţionale şi ştim ca dacă $\left \{ x;y \right \} d.p \left \{ 3;4 \right \}\Rightarrow \frac{x}{3}=\frac{y}{4}=k$

$\Rightarrow \frac{x}{3}=k \Rightarrow x=3k$

$\Rightarrow \frac{y}{4}=k \Rightarrow y=4k$

Dar problema ne spune că y este cu 14 mai mare decât x $\Rightarrow y=x +14$ .

Înlocuim în această ecuaţie pe x şi y în funţie de k şi obţinem:

$4k=3k +14 \Rightarrow 4k - 3k=14 \Rightarrow k=14.$

Înlocuim şi aflăm valoarea lui x şi a lui y.

$x=3k \Rightarrow x=3 \cdot12 \Rightarrow x=36$

$y=4k \Rightarrow y=4 \cdot12 \Rightarrow y=48$

Pentru scrierea formulei mărimilor direct proporţionale şi identificarea celor 2 numere în funcţie de k se acordă 2 puncte, iar obţinerea rezultatului corect al exercitiului se punctează cu 3 puncte.

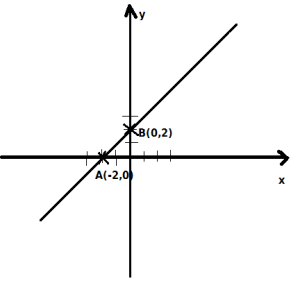
Se consideră funcţia $f :R \rightarrow R, f (x) = x - 5 .$

a) Calculați f (5) .

b) Reprezentați grafic funcția f într-un sistem de coordonate xOy.

Rezolvare:

a) Calculăm $f (5)= 5 - 5 = 0$

Pentru înlocuirea lui x cu (5) se punctează 3 puncte, iar pentru aflarea rezultatului corect se punctează cu 2 puncte.

b) Calculăm intersecţia funcţiei cu cele 2 axe Ox şi Oy după care trasăm graficul funcţiei.

$\cap OX \Rightarrow y = 0 \Rightarrow f(x) = 0\Rightarrow x - 5 = 0\Rightarrow x = 5\Rightarrow A(5 ; 0)$

$\cap Oy \Rightarrow x = 0\Rightarrow f(0) = 0 - 5\Rightarrow f(0) = -5 \Rightarrow B(0 ; -5)$

Pentru reprezentarea fiecarui punct A şi B care aparţine graficului funcţiei f se obţin câte 2 puncte, iar pentru trasarea graficului funcţiei f se punctează cu 1 punct.

Se consideră expresia $E(x) = (\frac{2}{x-1} - \frac{1}{x+1}) : \frac{(x+3)(x-1)}{x^2-2x+1}$ , unde x este număr real, x ≠-3 ,x ≠ -1 şi x ≠1. Arătați că E(x) = , pentru orice x număr real, x ≠ -3 , x ≠ -1 şi x ≠1.

Rezolvare: Pentru a rezolva expresia trebuie mai întâi să efectuăm operaţia de scădere din paranteză, apoi operaţia de împărţire dintre cele două fracţii. Pentru a efectua operaţia de scădere din paranteză trebuie să aducem la acelaşi numitor, astfel amplificăm prima fracţie din paranteză cu x+1 iar cea dea doua fracţie din paranteză o amplificăm cu x-1.

$E(x) = (\frac{2(x+1)}{(x-1)(x+1))} - \frac{x-1}{(x+1)(x+1)}) : \frac{(x+3)(x-1)}{x^2-2x+1}$

$E(x) = \frac{2x+2-x+1}{(x-1)(x+1)} : \frac{(x+3)(x-1)}{(x-1)^2}$

$E(x) = \frac{x+3}{(x-1)(x+1)} \cdot \frac{(x-1)^2}{(x+3)(x-1)}$

$E(x) = \frac{1}{x+1}$

Pentru aplicarea formulelor de calcul prescurtat şi pentru scoaterea factorului comun se obţin 3 puncte, iar pentru aflarea rezultatului corect al expresiei lui E(x) se punctează 2 puncte.

SUBIECTUL al III-lea - Pe foaia de examen scrieţi rezolvările complete.

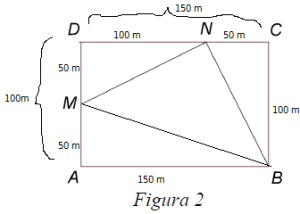
Figura 2este schiţa unui steag format din două trapeze dreptunghice ABCD și EFCD, AE ⊥ DC, în care AB = EF = 8dm , DC = 6 dm, AD = 2 dm și punctul D este mijlocul segmentului AE .

a)Arătați că aria trapezului ABCD este egală cu $14\sqrt{3} dm^{2}$ .

b) Calculaţi lungimea segmentului BF .

c) Arătați că unghiul BCF are măsura de 120° .

Demonstraţie:

a) Ştim că ABCD este trapez $\Rightarrow A_{ABCD}=\frac{(B+b)\cdot h}{2}$ $A_{ABCD}=\frac{(AB+CD)\cdot AD}{2}=\frac{(8 dm+6 dm)\cdot 2\sqrt{3}dm}{2}=\frac{14 dm \cdot 2\sqrt{3}dm}{2}=\frac{ 28\sqrt{3}dm}{2}=14\sqrt{3}dm^2$

Pentru enunţarea formulei ariei şi ]nlocuirea corectă a dimensiunilor se acordă 2 puncte, iar pentruobţinerea rezultatului corect al ariei se punctează cu 3 puncte.

b) $ABCD trapez \Rightarrow AB \parallel DC$

$DCEF trapez \Rightarrow EF \parallel DC$ $\Rightarrow$ $AB\parallel EF$ $AB\parallel EF$ $\Rightarrow$ ABFE paralelogram $\Rightarrow$ $BF \equiv AE$

$AE = AD + DE =2\sqrt{3} dm +2\sqrt{3} dm = 4\sqrt{3} dm\Rightarrow BF = 4\sqrt{3} dm$

Pentru demonstrarea ABFE paralelogram se acordă 2 puncte, iar pentruobţinerea rezultatului corect al lui BF se punctează cu 3 puncte.

$\Rightarrow m(<BCF)= 180^\circ -30^\circ-30^\circ=150^\circ -30^\circ= 120^\circ$

Pentru demonstrarea ∆CMB ∆CNF se acordă 2 puncte, iar pentru obţinerea rezultatului corect al unghiului se punctează cu 3 puncte.

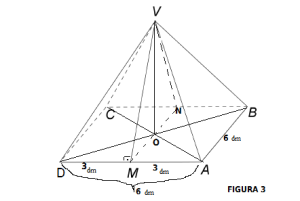
În Figura 3 este reprezentată o piramidă patrulateră regulată VABCD cu înălţimea de 4m şi latura bazei de 8m .

a) Arătaţi că perimetrul pătratului ABCD este egal cu 32m.

b) Arătaţi că aria laterală a piramidei VABCD este egală cu $64\sqrt{2}m^2$ .

c) Determinaţi măsura unghiului dintre planul unei feţe laterale a piramidei și planul bazei.

Demonstraţie:

a) Pentru a afla perimetrul pătratului facem suma laturilor. Ştim că laturile pătratului sunt egale deci putem scrie:

$P_{{ABCD}}=4\cdot l=4 \cdot8 m=32 m.$

Pentru identificarea dimensiunii laturilor se acordă 3 puncte, iar pentrucalcularea corectă a perimetrului se punctează cu 2 puncte.

b) $A_l= \frac{(P_b\cdot a_p)}{2}$

Ştim că M este mijlocul segmentului BC şi $\left \{ O \right \}=AC\cap BD$ ⇒∆VOM dreptunghic în <O.

Pentru a afla dimensiunea lui VM(apotema piramidei) aplicăm Teorema lui Pitagora în triunghiul dreptunghic VOM.

$\Delta VOM (<O = 90^\circ) : VM^2=VO^2 + OM^2$

$VM^2=4^2+4^2$

$VM^2 = 16 + 16 .$

$VM^2 = 32 .$

$VM = 4\sqrt{2} m$

$A_l= \frac{(P_b\cdot a_p)}{2} = \frac{(32 m \cdot 4\sqrt{2})}{2} = \frac{(128\sqrt{2})}{2} = 64\sqrt{2} m^2.$

Pentru calcularea corectă a dimensiuni laturii VM se acordă 2 puncte, iar pentru calcularea corectă a ariei laterale se punctează cu 3 puncte.

$\Delta VOM (<O = 90^\circ) : tg (<VMO) =\frac{VO}{OM} = \frac{4 dm}{4dm} = 1 \Rightarrow m(<VMO) = 45^\circ.$

Pentru demonstrarea unghiului dintre cele două plane se acordă 2 puncte, iar pentru calcularea corectă a unghiului dintre cele două plane se punctează cu 2 puncte.

Dragul meu părinte, sper din tot sufletul ca aceste informaţii să-ţi fie utile atunci când îţi ajuţi copilul să se pregătească şi să treacă cu bine peste examenul de capacitate din acest an.

Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimitre un e-mail la adresa:mathmoreeasy@yahoo.com

De asemenea, te invit şi pe pagina de facebook a blogului:

https://www.facebook.com/MathMoreEasy

Dragul meu părinte, mai sunt doar 10 zile până la Examenul de evaluare naţională proba de matematică din 29 iunie 2016 pentru elevii de clasa a VIII-a.

În articolul precedent am rezolvat şi explicat exerciţiile date la Sesiunea Speciala a Evaluării Naţionale 2016.

În acest articol voi aborda exerciţiile date la Evaluarea naţională sesiunea 2015.

(mai mult…)

Subiectul 1

Pe foaia de examen trebuie completat doar răspunsul corect în spaţiul punctate.

Rezultatul calculului 10 × 2 - 20 este egal cu … 0.

Rezolvare: Pentru că avem o operaţie de înmulţire şi o operaţie de scădere, facem întâi operaţia de înmulţire apoi scăderea si obţinem 20-20=0.

Dacă $\frac{a}{4}=\frac{3}{2}$ atunci "a" este egal cu ...6.

Rezolvare: Pentru al afla pe “a” facem produsul mezilor egal cu predusul extremilor şi obţinem:

$2 \cdot a=4\cdot3 .$

$2a=12 \Rightarrow a=12 \div 2 \Rightarrow a=6 .$

Cel mai mare număr natural care aparţine intervalului [1,5] este egal cu 5.

Rezolvare: Pentru că avem un interval închis (paranteza este pătrată) putem lua şi valoarea 5.

Pătratul ABCD are latura de 6 cm. Perimetrul pătratului ABCD este egal cu 24 cm .

Rezolvare: Ştim că perimetrul pătratului este suma tuturor laturilor. Dar laturile pătratului sunt egale.

$P_{ABCD}=4 \cdot l=4 \cdot6 cm=24 cm$

În Figura 1 este reprezentat un cub ABCDEFGH . Măsura unghiului determinat de dreptele AB și BF este egală cu $90^{\circ}$

Rezolvare: Ştim că ABFE este pătrat deci măsura unghiului determinat de dreptele AB şi BF este egală cu măsura ( $\lt ABF$ )= 90 °.

În diagrama de mai jos este prezentată repartiţia elevilor unei clase a VIII-a, în funcție de notele obţinute la teza de matematică pe semestrul al II-lea.

Numărul elevilor care au obţinut nota 10 este egal cu 3 elevi .

SUBIECTUL al II-lea - Pe foaia de examen scrieţi rezolvările complete.

Dragul meu părinte, acest subiect are in total 30 puncte. Spre deosebire de subiectul anterior, la acest subiect nu sunt punctate doar raspunsurile ci şi rezolvările şi formulele.

Pentru orice soluţie corectă, chiar dacă este diferită de cea din barem, se acordă punctajul corespunzător.
Nu se acordă fracţiuni de punct, dar se pot acorda punctaje intermediare pentru rezolvări parţiale, în limitele punctajului indicat în barem

Desenaţi, pe foaia de examen, un paralelipiped dreptunghic ABCDA'B'C'D

Pentru desenarea corectă a paralelipipedului se obţin 4 puncte, iar notarea corectă a cubului se punctează cu 1 punct.

Calculaţi media aritmetică a numerelor de două cifre, multipli ai lui 40.

Rezolvare: Stim din clasa a V-a că multiplul unui număr “d”este un numărul “m” obţinut prin înmulţirea lui “d” cu un număr natural.

Dragul meu părinte găseşti mai multe informaţii despre “Divizor. Multiplu” aici: http://mathmoreeasy.ro/divizor-multiplu/ .

Dar să revenim la exerciţiul nostru şi să vedem care sunt multiplii numărului 40.

$40\cdot1=40$

$40\cdot2=80$

$40\cdot3=120$

$40\cdot 4=160$

…………

Dar exerciţiul ne cere multiplii de două cifre ai lui 40. Observăm că doar numerele 40 şi 80 îndeplinesc condiţiile impuse de exerciţiul aşa că vom calcula media aritmetică a celor două numere 40 şi 80.

$M_{a}=\frac{a+b}{{2}}=\frac{40+80}{{2}}=\frac{120}{{2}}=60$

Pentru scrierea formulei mediei aritmetice şi identificarea celor 2 multipli 3 puncte, iar obţinerea rezultatului corect al exercitiului se punctează cu 2 puncte.

Se acordă punctajul maxim şi în cazul în care candidaţii au luat în considerare şi multiplii negativi de două cifre, iar media aritmetică este calculată corect.

Mihai a cheltuit o sumă de bani în două zile. În prima zi Mihai a cheltuit 30% din sumă, iar în a doua zi restul de 35 de lei. Calculați suma de bani cheltuită de Mihai în prima zi.

Rezolvare: Pentru că nu ştim suma iniţială de bani o vom nota cu x.

Notăm: x= suma de bani iniţială.

$\frac{30}{{100}}\cdot x=\frac{3x}{{10}}$ (a cheltuit Mihai în prima zi)

$x- \frac{3x}{{10}}=35 lei$

Pentru a putea face calculele aducem la acelaşi numitor, astfel îl amplificăm pe x cu 10 şi obţinem :

$\frac{10x-3x}{{10}}=35 lei$

$\frac{7x}{{10}}=35 lei$

$x= \frac{35 lei \cdot10}{{7}}= 50 lei$ (a avut Mihai iniţial)

$\frac{3}{{10}}\cdot 50 lei= 15 lei$ ( a cheltuit Mihai în prima zi).

Pentru notarea sumei de bani se acordă 1 punct , pentru scrierea ecuaţiei exerciţiului se punctează 2 puncte, iar pentru aflarea corectă a sumei cheltuita în prima zise punctează cu 2 puncte.

Se consideră funcţia f :ℝ $\rightarrow$ ℝ, f (x) = x+2.

a) Calculați f (-2) .

b) Reprezentați grafic funcția f într-un sistem de coordonate xOy .

Rezolvare:

a) Calculăm $f (-2)= -2 +2 = 0$

Pentru înlocuirea lui x cu (- 2) se punctează 3 puncte, iar pentru aflarea rezultatului corect se punctează cu 2 puncte.

b) Calculăm intersecţia funcţiei cu cele 2 axe Ox şi Oy după care trasăm graficul funcţiei.

$\cap OX$ : $y = 0 \Rightarrow f(x) = 0 \Rightarrow x +2 = 0 \Rightarrow x = - 2 \Rightarrow A(-2 ; 0)$

$\cap Oy$ : $x = 0\Rightarrow f(0) = 0 +2 \Rightarrow f(0) = 2 \Rightarrow B(0 ; 2)$

Pentru reprezentarea fiecarui punct A şi B care aparţine graficului funcţiei f se obţin câte 2 puncte, iar pentru trasarea graficului funcţiei f se punctează cu 1 punct.

Se consideră expresia $E(x) = \frac{x^2-49}{{x^2-7x}}- \frac{2x-7}{{x^2+x}} : \frac{1}{{x+1}}$ , unde x

este număr real, x ≠ -1, x ≠ 0 şi x ≠7. Arătaţi că E(x) = -1, pentru orice x număr real, x ≠ -1,x ≠ 0 şi x≠ 7 .

Rezolvare: Pentru a rezolva expresia trebuie mai întâi să efectuăm operaţia de împărţire dintre ultimele două fracţii, iar în prima fracţie aplicăm la numărător formula de calcul prescurtat : $a^{{2}}-b^{{2}}=(a-b)(a+b)$ , iar la numitor dăm factor comun pe x.

$E(x) = \frac{(x-7)(x+7)}{{x(x-7)}}- \frac{2x-7}{{x(x+1)}} \cdot \frac{x+1}{{1}}$

$E(x) = \frac{(x+7)}{{x}}- \frac{2x-7}{{x}}$

$E(x) = \frac{(x+7-2x-7)}{{x}}$

$E(x) = \frac{(-x)}{{x}}$

$E(x) = -1$

Pentru aplicarea formulelor de calcul prescurtat şi pentru scoaterea factorului comun se obţin 3 puncte, iar pentru aflarea rezultatului corect al expresiei lui E(x) se punctează 2 puncte.

SUBIECTUL al III-lea - Pe foaia de examen scrieţi rezolvările complete. (30 puncte)

Figura 2 este schiţa unui teren în formă de dreptunghi ABCD cu AB =150m şi AD =100m . Punctul M este mijlocul laturii AD , iar punctul N este situat pe latura DC astfel încât DN = 2NC.

a) Arătați că aria terenului ABCD este egală cu 1,5ha .

b) Demonstrați că triunghiul MNB este isoscel.

c) Calculați măsura unghiului format de dreptele MN și NB.

Demonstraţie:

a) Ştim că ABCD este dreptunghi ⇒ $A_{{ABCD}}= L\cdot l = 150 m \cdot 100 m = 15000 m^{2}$

Transformăm $m^{2}$ în ha împărţind la 10 000.

Obţinem astfel: $A_{ABCD}=15000 m^{2} =1,5 ha$

Pentru enunţarea formulei ariei şi calcularea corectă a ariei se acordă 2 puncte, iar pentrutransformarea din în ha se punctează cu 3 puncte.

b) Pentru a demonstra că ∆MNB este triunghi isoscel este suficient să arătăm că laturile MN şi NB sunt congruente.

Aplicăm Teorema lui Pitagora în triunghiurile dreptunghice MDN şi BCN şi calculăm MN şi NB.

$\Delta MDN(<D= 90^{\circ} )$ : $MN^2= MD^2 + DN^2$

$MN^2 = 50^2 + 100^2$

$MN^2 = 2500 + 10 000$

$MN^2 = 12500$

$MN = \sqrt{12500}$

$MN = 50\sqrt{5} m$

$\Delta NCB(<C= 90^{\circ} )$ : $NB^2= NC^2 + BC^2$

$NB^2 = 50^2 + 100^2$

$NB^2 = 2500 + 10 000$

$NB^2 = 12500$

$NB=\sqrt{12500}$

$NB=50\sqrt{5}m$

⇒ MN $\equiv$ NB ⇒ ∆ MNB isoscel

Pentru identificarea egalităţii laturilor MN şi NB se acordă 3 puncte, iar pentru demonstrarea triunghiului MNB isoscel se punctează cu 2 puncte.

c) Pentru a calcula măsura unghiului dintre dreptele MN şi NB vom verifica mai întâi dacă ∆MNB este dreptunghic isoscel, folosind Reciproca teoremei lui Pitagora. Calculăm latura MB din tringhiul dreptunghic MAB.

$\Delta MAB$ $(<A= 90^{\circ} )$ : $MB^2= MA^2 + NB^2$

$MB^2 = 50^2 + 150^2$

$MB^2 = 2500 + 22 500$

$MB^2 = 25000$

$MB=\sqrt{25000}$

$MB=50\sqrt{10}m$

$\Delta MNB$ : $MB^2= MN^2 + NB^2$

$(50\sqrt{10})^2=(50\sqrt{5})^2+(50\sqrt{5})^2$

$25 000 = 12500 + 12 500$

$25 000 = 25 000$ $\Rightarrow \Delta MNB$ dreptunghic isoscel
$\Rightarrow m(<MNB) =90^\circ$ .

Pentru identificarea $<MNB= 90^\circ$ se punctează cu 5 puncte.

În Figura 3 este reprezentată o piramidă patrulateră regulată VABCD cu VA = $3\sqrt{5}$ dm și AB = 6dm . Punctul M este mijlocul laturii AD

a)Arătaţi că VM = 6 dm.

b) Calculaţi câte grame de vopsea sunt necesare pentru vopsirea suprafeței laterale a piramidei, știind că pentru vopsirea unei suprafeţe de un decimetru pătrat se folosesc 30 grame de vopsea.

c) Demonstrați că sinusul unghiului dintre planele (VAD) și (VBC) este egal cu .

Demonstraţie:

a) Ştim că $VA\equiv VD\Rightarrow \Delta VAD isoscel \Rightarrow VM\perp AD$ . Pentru a afla dimensiunea lui VM aplicăm Teorema lui Pitagora în triunghiul dreptunghic VMD.

$\Delta VMD (<M = 90^\circ )$ : $VD^2=DM^2 + VM^2$

$VM^2=(3\sqrt{5})^2-(3)^2$

$VM^2=45-9$

$VM^2=36$

$VM =\sqrt{36}$

$VM =6 dm$

Pentru identificarea dimensiunii laturilor se acordă 2 puncte, iar pentrucalcularea corectă a lui VM se punctează cu 3 puncte.

b) La punctual b) trebuie să calculăm aria laterală a piramidei.

$A_l=\frac{P_b \cdot a_p{}}{{2}}$ = $\frac{24 dm \cdot 6 dm{}}{{2}}$ = $\frac{144 dm^2{}}{{2}}$ =72 $dm^2$ .

$P_{{b}}=4\cdot l =24 dm$

Apotema piramidei $a_{{p}}=VM$

72 ·30g = 2160g = 2,16 kg.

Pentru formula ariei şi calcularea corectă a ariei se acordă 3 puncte, iar pentru calcularea corectă gramajului vopselei se punctează cu 2 puncte.

c) Ştim că AD $\parallel$ BC şi

VABCD piramidă patrulateră regulată ⇒ ∆ VBC isoscel ⇒VN ⊥ BC

Pentru identificarea si demonstrarea unghiului dintre cele 2 plane se acordă 3 puncte, iar pentru calcularea corectă a măsurii unghiului se punctează cu 2 puncte.

Dragul meu părinte, sper din tot sufletul ca aceste informaţii să-ţi fie utile atunci când îţi ajuţi copilul să se pregătească şi să treacă cu bine peste examenul de capacitate din acest an.

Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimitre un e-mail la adresa:mathmoreeasy@yahoo.com

De asemenea, te invit şi pe pagina de facebook a blogului:

Matematica Mai Usoara

Categorie: Subiecte rezolvate Evaluare Naţionala 2015

Evaluare Naţională Sesiunea Specială pentru Olimpici 2015

Dragul meu părinte, sper din tot sufletul ca aceste informaţii să-ţi fie utile atunci când îţi ajuţi copilul să se pregătească şi să treacă cu bine peste examenul de capacitate din acest an.

Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimitre un e-mail la adresa:mathmoreeasy@yahoo.com

De asemenea, te invit şi pe pagina de facebook a blogului:

https://www.facebook.com/MathMoreEasy

Subiecte Evaluare naţională 2015

Pentru identificarea si demonstrarea unghiului dintre cele 2 plane se acordă 3 puncte, iar pentru calcularea corectă a măsurii unghiului se punctează cu 2 puncte.

Dragul meu părinte, sper din tot sufletul ca aceste informaţii să-ţi fie utile atunci când îţi ajuţi copilul să se pregătească şi să treacă cu bine peste examenul de capacitate din acest an.

Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimitre un e-mail la adresa:mathmoreeasy@yahoo.com

De asemenea, te invit şi pe pagina de facebook a blogului:

https://www.facebook.com/MathMoreEasy