Dragul meu părinte, bine te-am regăsit.
Dragul meu părinte, bine te-am regăsit.
Nu am mai scris nimic de mult timp şi pentru că se apropie cu paşi repezi examenul de capacitate pentru absolvenţii clasei a VIII-a m-am gândit în articolul de azi să rezolvăm exerciţiile date la sesiunea specială pentru olimpici care s-a desfăşurat săptămâna trecută.
Voi rezolva şi explica fiecare exerciţiu pas cu pas, menţionând şi punctajul aferent fiecarui exerciţiu conform baremului de corectare, astfel ca ţie să-ţi fie uşor să-i explici copilului tău cum să rezolve şi să trateze fiecare exerciţiu pentru a obţine un punctaj cât mai mare la examenul de capacitate care va avea loc pe data de 29 iunie 2016. (mai mult…)
Subiectul 1
Pe foaia de examen trebuie completat doar răspunsul corect în spaţiul punctat.
-
1. Rezultatul calculului 10×5 - 10 este egal cu …40 .
Rezolvare: 10×5 - 10 = 50-10 = 40
-
2. Șase cărți de acelaşi fel costă în total 24 de lei. Trei dintre aceste cărți costă în total ..12 lei.
Rezolvare: Această problemă poate fi rezolvată in mai multe moduri:
Metoda I. 24 : 6=4 (Lei costă o carte)
3 x 4=12 (Lei costă 3 cărti)
Metoda II. Folosind Regula de trei simplă:
6 cărţi……………………24 lei
3 cărţi……………………x lei
x = %7D%7B6%7D%20%3D%5Cfrac%7B72%7D%7B6%7D%3D12) lei
lei
-
3. Cel mai mic număr natural care aparţine intervalului [1, 4] este egal cu …1 .
Rezolvare: Pentru că avem un interval închis (paranteza este pătrată) putem lua şi valoarea 1.
-
4. Dreptunghiul ABCD are AB = 5 cm și BC = 3 cm. Aria acestui dreptunghi este egală cu …15
Rezolvare: Ştim că aria dreptunghiului este produsul dintre lungime şi lăţime.
A=L x l = 5 cm x 3 cm= 15 
-
5. În Figura 1 este reprezentat un paralelipiped dreptunghic ABCDA'B'C'D'. Măsura unghiului determinat de dreptele AD şi AA' este egală cu ..90 ° .
Rezolvare: Ştim că A'ADD' este dreptunghi deci măsura unghiului determinat de dreptele AD şi AA' este egală cu măsura (<A'AD)= 90 °.
-
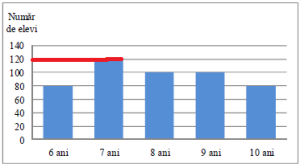
6. În diagrama de mai jos este prezentată repartiţia după vârstă a elevilor unui club sportiv.Numărul elevilor acestui club sportiv care au vârsta de 7 ani este egal cu ...120.
- Se punctează doar rezultatul, astfel: pentru fiecare răspuns se acordă fie 5 puncte, fie 0 puncte.
- Nu se acordă punctaje intermediare.
SUBIECTUL al II-lea
-
Pe foaia de examen scrieţi rezolvările complete.
-
Pentru orice soluţie corectă, chiar dacă este diferită de cea din barem, se acordă punctajul corespunzător.
-
Nu se acordă fracţiuni de punct, dar se pot acorda punctaje intermediare pentru rezolvări parţiale, în limitele punctajului indicat în barem.
Dragul meu părinte, acest subiect are in total 30 puncte. Spre deosebire de subiectul anterior, la acest subiect nu sunt punctate doar raspunsurile ci şi rezolvările şi formulele.
-
1. Desenaţi, pe foaia de examen, un cub ABCDEFGH .
Pentru desenarea corectă a cubului se obţin 4 puncte, iar notarea corectă a cubului se punctează cu 1 punct.
-
2. Știind că
, unde a și b sunt numere reale nenule, arătați că
%7D%7Bb%7D%3D10) .
.
Rezolvare: Şi această problemă are 2 metode de rezolvare:
Metoda I. Scriem 4 ca fracţie cu numitorul 1 şi îl scoatem pe "a" în funcţie de "b".

%7D%7Bb%7D%3D10%0A) .
.
%7D%7Bb%7D%3D10%0A)
%7D%7Bb%7D%3D10) .
.

)
Metoda II. Scoatem factor comun forţat pe b din a doua ecuaţie.
b se simplifică şi obţinem:
 .
.
%3D10) .
.
 (A)
(A)
Pentru efectuarea substituţiei sau a scoaterii factorului comun se obţin 3 puncte, iar obţinerea rezultatului corect al exercitiului se punctează cu 2 puncte.
-
3. Preţul unui obiect este de 360 lei. După o reducere cu p% din preţul obiectului, noul preț va fi de 324 lei. Determinați numărul p .
Rezolvare:
Aflam întâi suma cu care s-a ieftinit produsul.
 .
.
 .
.
 .
.
Pentru aflarea sumei cu care s-a ieftinit produsul se obţin 2 puncte, iar pentru scrierea corecta a ecuaţiei lui p si obţinerea rezultatului corect se punctează cu 3 puncte.
-
4. Se consideră funcţia f :ℝ →ℝ, f (x) = x - 4 .
a) Reprezentați grafic funcția f într-un sistem de coordonate xOy .
b) Arătaţi că triunghiul determinat de graficul funcției f și axele sistemului de coordonate xOy este isoscel.
Rezolvare:
Calculăm intersecţia funcţiei cu cele 2 axe Ox şi Oy după care trasăm graficul funcţiei.
Pentru reprezentarea fiecarui punct M şi N care aparţine graficului funcţiei f(x) se obţin câte 2 puncte, iar pentru trasarea graficului funcţiei f(x) se punctează cu 1 punct.
-
b) Arătaţi că triunghiul determinat de graficul funcției f și axele sistemului de coordonate xOy este isoscel.
Rezolvare: Segmentele OM = 4 u şi ON = 4 u → OM ≡ ON → triunghiul MON isoscel.
Pentru determinarea dimensiunilor fiecarui segment OM şi ON care aparţine graficului funcţiei f(x) se obţin câte 2 puncte, iar pentru demonstrarea triunghiului isoscel se punctează cu 1 punct.
-
5. Se consideră expresia :
%3D(%5Cfrac%7Bx%2B2%7D%7Bx-3%7D-%5Cfrac%7Bx-3%7D%7Bx%2B2%7D-%5Cfrac%7B25%7D%7B(x%2B2)(x-3)%7D)%20%3A%20%5Cfrac%7B5%7D%7Bx%2B2%7D) , unde x este număr real,
, unde x este număr real,
x ≠ -2 şi x ≠ 3. Arătați că E(x) = 2 , pentru orice x număr real, x ≠ -2 şi x ≠ 3.
Rezolvare: Pentru a rezolva expresia trebuie mai întâi să aducem la acelaşi numitor în paranteză şi să rezolvăm paranteza aplicând formulele de calcul prescurtat :
Simplificăm termenii asemenea şi obţinem:
Pentru aducerea la acelaşi numitor şi aplicarea formulelor de calcul prescurtat se obţin 3 puncte, iar pentru aflarea rezultatului corect al expresiei lui E(x) se punctează cu 2 puncte.
SUBIECTUL al III-lea
Pe foaia de examen scrieţi rezolvările complete. (30 puncte)
-
1. Figura 2 este schiţa unui teren. ABCD și BEFC sunt paralelograme cu AD=60m, AB = BE = 80m și punctele A, B și E coliniare. Se consideră punctele M și N pe laturile BE, respectiv CD, astfel încât MN
BC și BM = CN = 60 m .
 a) Arătați că perimetrul paralelogramului ABCD este egal cu 280 m.
a) Arătați că perimetrul paralelogramului ABCD este egal cu 280 m.
b) Demonstrați că unghiul DAB are măsura de 60° .
c) Demonstrați că aria suprafeței CMEF este mai mică decât 2600 m2 .
Rezolvare:
a) Notăm cu  =AB=DC laturile mari ale paralelogramului şi cu
=AB=DC laturile mari ale paralelogramului şi cu  = AD=BC
= AD=BC
laturile mici ale paralelogramului.
Pentru scrierea şi aplicarea formulei perimetrului dreptunghiului se obţin 2 puncte, iar pentru aflarea rezultatului corect al perimetrului se punctează cu 3 puncte.
b) Ştim din datele problemei ca  şi ca
şi ca  deoarece ABCD şi BEFC sunt paralelograme
deoarece ABCD şi BEFC sunt paralelograme BMNC paralelogram şi pentru ca
BMNC paralelogram şi pentru ca 


 BN≡CN=60m.
BN≡CN=60m.
Dar ABCD paralelogram 


 .
.
În concluzie am demonstrat ca 



%3D%20%2060%5E%7B%5Ccirc%7D) .
.
Dar ABCD paralelogram 
%5Cequiv%20m%20(%3CDAB))

%3D%20%2060%5E%7B%5Ccirc%7D) .
.
Pentru demonstrarea că  se obţin 2 puncte, iar pentru aflarea măsurii unghiului
se obţin 2 puncte, iar pentru aflarea măsurii unghiului %3D%20%2060%5E%7B%5Ccirc%7D) se punctează cu 3 puncte.
se punctează cu 3 puncte.
c) Observăm ca MEFC este trapez, iar pentru a calcula Aria trapezului avem nevoie de înălţimea trapezului.
În cazul nostru  iar
iar  . Pentru a afla dimensiunea lui EP aplicăm teorema lui Pitagora în triunghiul ∆ EPF.
. Pentru a afla dimensiunea lui EP aplicăm teorema lui Pitagora în triunghiul ∆ EPF.
Ştim 
.%20Dar%20%3C%20EFP%20%3D%2060%5E%7B%5Ccirc%7D%20%5CRightarrow%20m(%20%3C%20PEF)%20%3D%2030%5E%7B%5Ccirc%7D%20%5CRightarrow%20PF%20%3D%20%5Cfrac%7BEF%7D%7B2%7D%3D%20%5Cfrac%7B60%7D%7B2%7D%3D30%20m)
%20) :
: 


 = 3600 – 900
= 3600 – 900



Pentru demonstrarea şi calcularea distanţei de la M la CF se obţin 2 puncte, iar pentru calcularea ariei şi demonstrarea rezultatului corect se punctează cu 3 puncte.
-
2. În Figura 3 este reprezentată o piramidă triunghiulară regulată VABC , cu baza triunghiul ABC și AB =12m . Punctul M este mijlocul segmentului BC și VM =
, iar VO este înălțimea piramidei.
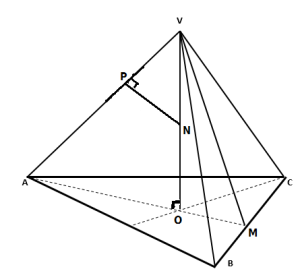
a) Arătați că aria laterală a piramidei VABC este egală cu  .
.
b) Arătați că volumul piramidei VABC este egal cu  .
.
c) Demonstrați că distanța de la mijlocul înălțimii VO la dreapta VA este mai mică decât 3m .
Rezolvare:
-
a) Pentru a afla aria laterală a piramidei regulate VABC aplicam formula:

Pentru că este piramidă regulată triunghiul de la bază ABC este triunghi echilateral deci toate laturile triunghiului sunt egale cu 12.
Obţinem astfel:  , iar apotema piramidei ne-o spune problema
, iar apotema piramidei ne-o spune problema
VM= .
.
Pentru scrierea formulei ariei laterale a piramidei triunghiulare regulate se obţin 2 puncte, iar pentru calcularea corectă a rezultatului ariei se punctează cu 3 puncte.
-
b) Pentru a afla volumul piramidei regulate VABC aplicam formula:

Pentru că este piramidă triunghiulară regulată aflăm aria triunghiului de la bază ABC cu ajutorul formulei:

Pentru a afla volumul piramidei regulate VABC avem nevoie şi de dimensiunea înălţimei piramidei VO.
Pentru a calcula înălţimea piramidei VO avem nevoie de dimensiunea laturei OM care stim ca este egală cu 1/3 din AM.
AM este înălţime în triunghiul echilateral ABC şi pentru ai afla dimensiunea aplicăm formula :
Calculăm înălţimea VO aplicând teorema lui Pitagora în triunghiul dreptunghic VOM.
∆VOM(< O =  ) :
) : 
%20%5E%7B%7B2%7D%7D%3DVO%5E2%20%2B(2%5Csqrt%7B3%7D)%20%5E%7B%7B2%7D%7D%0A%0A)



Pentru aflarea dimensiunii înălţimii piramidei se obţin 2 puncte, iar pentru scrierea formulei volumului piramidei triunghiulare regulate şi calcularea corectă a volumului se punctează cu 3 puncte.
-
c) Ştim că N mijlocul lui VO şi NP este distanţa de la N la VA → NP ⊥ VA (P ɛ VA) → că ∆VPN este asemenea cu ∆VOA conform criteriului de asemămare U.U obţinem următoarele rapoarte egale:
∆VPN ~ ∆VOA → 
Din aceste rapoarte egale putem să scoatem dimensiunea laturii NP.
Pentru a afla NP avem nevoie de dimensiunea muchiei VA care ştim că este egală cu muchia VB.
Aflăm VB din triunghiul dreptunghic VMB cu ajutorul teoremei lui Pitagora.
∆VMB (< M =  )
) 
Pentru ca N este mijlocul lui VO →  .
.
Dar noi trebuie să demonstrăm ca NP < 3m 
8 < 9 (A)
Pentru identificarea corectă a rapoartelor lui Thales se obţin 2 puncte, iar calcularea corectă a dimensiunii laturii NP şi demonstraţia ca  se punctează cu 3 puncte.
se punctează cu 3 puncte.
Se acordă 10 puncte din oficiu. Nota finală se calculează prin împărţirea la 10 a punctajului total obținut pentru lucrare.