functii - Matematica Mai Usoara

"Nu îmi învăț niciodată studenții; tot ce fac este să le creez condițiile pentru ca ei să învețe."
Albert Einstein

Dragul meu părinte bine te-am găsit!

Azi te invit să exersăm împreună câteva exerciții la Graficul unei Funcții! (mai mult…)

Exercițiul 1:

Fie funcția $f \ \ \ : \ \ \ R \rightarrow R ,$ $f (x)=-2x+1$ .

a) Reprezentați grafic funcția.

b)Determinați numărul real $a \in R,$ știind că punctul $A(2a-1,\ \ \ a-2)$ este situate pe graficul funcției f(x).

c) Calculați suma $S=f(0)+f(1)+f(2)+..........+f(2011)$

Rezolvare:

a) Pentru a obține punctul în care graficul funcției intersectează axa OX punem condiția ca $y=0 \Rightarrow f(x)=0$ .

$\cap OX$ : $y=0 \Rightarrow f(x)=0 \Rightarrow$ $-2\cdot x+ 1=0$

$\Rightarrow$ $-2\cdot x=-1$ $\Rightarrow$ $x=\frac{-1}{{-2}}$

$\Rightarrow$ $x=\frac{1}{{2}}$ $\Rightarrow A( \frac{1}{{2}} \ ; 0)$

Pentru a obține punctul în care graficul funcției intersectează axa OX punem condiția ca $x=0$
$\cap OY:$ $x=0$ $\Rightarrow$ $f(0)= -2\cdot 0+ 1 = 1$
$B(0\ \ ;\ \ \ 1)$

b) Pentru a arăta că punctul $A(2a-1,\ \ \ a-2)$ aparține graficului funcției f(x) punem condiția ca : $f(2a-1)= a-2$ adică în forma funcției f(x) înlocuim x cu 2a-1 și obținem:

$f(2a-1)= a-2$ $\Rightarrow -2\cdot (2a-1) + 1 = a-2$ $\Rightarrow -4\cdot a+2 + 1 = a-2$

$\Rightarrow -4a+3 = a-2$

Trecem toți termenii cu a într-o parte și toți termenii fară a în cealaltă parte.

$\Rightarrow -4a-a=-2-3$ $\Rightarrow -5a=- 5 \ \ \ \ /:(-5)$ $\Rightarrow a= 1$

c) $S=f(0)+f(1)+f(2)+... . . . . + f(2011)$

Calculăm $f(0), f(1), f(2), . . . . . , f(2011)$ și observăm că obținem Suma Gauss.

$f(0)= -2 \cdot 0 + 1= 0+1=1$

$f(1)= -2 \cdot 1 + 1= - 2 +1= -1$

$f(2)= -2 \cdot 2 + 1= - 4 +1= -3$

. . . . . . .. .. . . . . . . .. . .. . . . .. . . . . . . .. . . . .

$f(2011)= -2 \cdot 2011 + 1= - 4 022+1= -4021$

Obținem :

$S= 1-1-3-5-. . .. . . . -4021$ $\Rightarrow S= -(3+5+. . .. . . . +4021)$

Aplicăm Suma Gauss a numerelor impare :

$n= (4021-3) \ \ \ : \ \ \ 2 +1$ $\Rightarrow n= 4018 \ \ \ : \ \ \ 2 +1$ $\Rightarrow n= 2009 +1 = 2010 (termeni)$

$S=-[2010\cdot (4021+3) \ \ \ : \ \ \ 2]$

$S=-[2010\cdot 4024 \ \ \ : \ \ \ 2]$

$S=-[2010\cdot 2012]$

$S=- 4 044 120$

Exercițiul 2:

Se consideră funcția $f : R\rightarrow R$ , $f(x)= -\sqrt{3}x+2\sqrt{3}$

a) Reprezentați grafic funcția

b) Determinați aria triunghiului format de graficul funcției și axele de coordinate.c

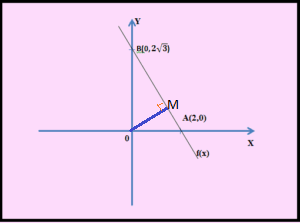
c) Determinați distanța de la punctul $O(0,0)$ la graficul funcției f(x).

Rezolvare:

a) $\cap OX :$ $y=0 \Rightarrow f(x)=0 \Rightarrow$ $-\sqrt{3}\cdot x+2\sqrt{3} = 0$

$\Rightarrow$ $-\sqrt{3}x=-2\sqrt{3}$

$\Rightarrow$ $x=\frac{2\sqrt{3}}{\sqrt{3}}$

$\Rightarrow$ $x= __{{}}^{\sqrt{3})}\textrm{\frac{2\sqrt{3}}{\sqrt{3}} }$

$\Rightarrow$ $x=2$ $\Rightarrow A(2\ \ \ ; \ \ \ 0 )$

$\cap OY:$ $x=0$ $\Rightarrow$ $f(0)= -\sqrt{3}\cdot 0+2\sqrt{3} = 2\sqrt{3}$
$\Rightarrow B(0 , 2\sqrt{3})$

b) Calculăm $A_{\bigtriangleup AOB }$ . Observăm că $\bigtriangleup AOB$ este dreptunghic în unghiul O astfel putem aplica formula:

$A_{{\bigtriangleup AOB}}= \frac{c_{1}\cdot c_{2}}{2}= \frac{OA\cdot OB}{2}= \frac{2\cdot 2\sqrt{3}}{2}=2\sqrt{3} u.m^{{2}}$

c) Știm că distanța de la un punct la o dreaptă este perpendiculara din acel punct pe dreaptă. Adică înălțimea triunghiului AOB. Pentru a afla înălțimea ne folosim de aria triunghiului pe care am calculate-o deja. Folosim formula:

$A_{\triangle AOB}= \frac{b \cdot h}{{2}}$ $= \frac{AB \cdot OM}{{2}}$

Calculăm AB cu formula distanței dintre punctele $A(2,0)$ și $B(0, 2\sqrt{3})$ astfel:

$AB= \sqrt{(x_{{B}}-x_{{A}})^2+(y_{{B}}-y_{{A}})^2}$

$x_{{A}}=2$ și $y_{{A}}=0$ iar $x_{{B}}=0$ și $y_{B}=2\sqrt{3}$ , înlocuim in formula și obținem:

$AB=\sqrt{(x_{{B}}-x_{{A}})^2+(y_{{B}}-y_{{A}})^2}$

$AB=\sqrt{{(2-0})^2+(2\sqrt{3}-0})^2}}$ $\Rightarrow AB=\sqrt{{2^2+(2\sqrt{3})^2}}$

$\Rightarrow AB=\sqrt{{4+2^2 \cdot 3}}$ $\Rightarrow AB=\sqrt{{4+12}}$ $\Rightarrow AB=\sqrt{{16}} = 4$

Înlocuim în formula ariei și aflăm OM.

$2\sqrt{3}u.m^2= \frac{4 u.m \cdot OM}{2} \ \ \ \ \ / \cdot 2$

$2 \cdot 2\sqrt{3}u.m^2= 4 u.m \cdot OM$ $\Rightarrow 4\sqrt{3}u.m^2= 4 u.m \cdot OM \ \ \ \ / \ \ : \ \ 4 u.m$

$\Rightarrow OM = \sqrt{3} \ \ u.m$

PS: Dragul meu părinte am pregătit si o Fișă de lucru cu Exerciții la Graficul unei funcții pentru copilul tău o gasești aici:Fisa de lucru Graficul unei functii

Dragul meu părinte, sper din tot sufletul ca aceste informații să îți

fie utile atunci când îți ajuți copilul la temele pentru acasă la matematică.

Dacă dorești să ai acces la mai multe exemple de exerciții cu un

grad de dificultate ridicat rezolvate și explicate pas cu pas te

invit să te înscrii în “Clubul de Matematică Math More Easy.”

Şcoala trebuie să te înveţe a fi propriul tău dascăl, cel mai bun şi cel mai aspru.

Nicolae Iorga

Dragul meu părinte bine te-am regăsit! A început școala iar perioada următoare este pentru toți elevi una solicitantă deoarece urmează perioada tezelor. Așa că azi îți propun un model de teză rezolvat și explicat pas cu pas pe înțelesul tuturor, dar și un model nerezolvat (asemănător) pe care copilul tău să îl rezolve singur urmărind modelul rezolvat de mine.

(mai mult…)

Model Propus Teza clasa a VIII-a Semestrul II

Subiectul I (total 4,5 puncte):

Exercițiul 1 (0,5 puncte):

Rezultatul calculului: $\sqrt{2} \cdot \sqrt{3}-3\sqrt{6}$ este:……………………………

Rezolvare:

$\sqrt{2} \cdot \sqrt{3}-3\sqrt{6}$ $=\sqrt{2\cdot 3}-3\sqrt{6}$ $=\sqrt{6}-3\sqrt{6}$ $=-2\sqrt{6}$

Exercițiul 2 (1 punct):

Simplificând cu $x^2+1$ raportul : $\frac{x^4-1}{{x^2+1}}$ se obține:.....................................

Rezolvare:

Aplicăm formulele de calcul prescurtat pentru expresia: $x^4-1$ și se obține:

$\frac{x^4-1}{{x^2+1}}=$ $\frac{(x^2)^2-1^2}{{x^2+1}}=$ $\frac{(x^2-1)(x^2+1)}{{x^2+1}}=$ $\frac{(x^2-1)(x^2+1)}{{x^2+1}}^{(x^2+1}=$ $\frac{x^2-1}{1}$ $=x^2-1$ .

Exercițiul 3 (1 punct):

Soluția ecuației: $x-\sqrt{3}=0$ este: ........................................

Rezolvare:

$x-\sqrt{3}=0$ $\Rightarrow x-\sqrt{3}=0 /-\sqrt{3}$ $\Rightarrow x=-\sqrt{3}$

Exercițiul 4 (1 punct):

Se considera funcția $f : R \to R$ , $f (x)=x-3$ . Valoarea funcției în punctul x=3 este egală cu: .........................

Rezolvare:

Pentru a afla valoarea functiei în punctul x=3 calculăm $f (3)$ (îl înlocuim pe x cu 3 în funcție.

$f (3)=3-3=0$

Exercițiul 5 (1punct):

Volumul cubului cu lungimea diagonalei de $\sqrt{12}cm$ este: ........................

Rezolvare:

Știm că diagonala cubului este egală cu:

$d=l\sqrt{3}\Rightarrow$ $l\sqrt{3}=\sqrt{12}\Rightarrow$ $l\sqrt{3}=\sqrt{4\cdot3}\Rightarrow$ $l\sqrt{3}=2\sqr{3}\Rightarrow$ $l\sqrt{3}=2\sqr{3} / :\sqr{3} \Rightarrow$ $l=2 cm$

Știm că volumul cubului are formula: $V= l^3$ ; înlocuim latura cu 2 cm și obținem:

$V= l^3 \Rightarrow$ $V= (2cm)^3 \Rightarrow$ $V= 8cm^3$ .

Subiectul II: (total 4,5 puncte):Pe foaia de examen se trec rezolvarile complete.

Exercițiul 1 (1,5 puncte):

Se consideră expresia: $E(x)=(1-x+\frac{x^2+1}{x-2}) : \frac{3x-1}{x-2}$ .

a) Determina'i valorile reale ale lui x pentru care expresia E(x) este bine definită.

b) Demonstrați că E(x)=1, $(\forall ) x \in R \setminus \left \{ -2; 1\right \}$ .

Rezolvare:

$E(x)=(1-x+\frac{x^2+1}{x-2}) : \frac{3x-1}{x-2}$ $\Rightarrow E(x)=(1-x+\frac{x^2+1}{x-2})\cdot \frac{x-2}{3x-1}$

a)Punem condițiile de existență ale fracțiilor (numitorul fracției trebuie să fie diferit de 0):

$x-2 \neq 0 \Rightarrow x \neq 2$

$3x-1 \neq 0 \Rightarrow 3x \neq 1$ $\Rightarrow 3x \neq \frac{1}{{3}}$

$\Rightarrow x \in R\setminus \left \{ \frac{1}{{3}} , 2 \right \}$

$E(x)=(1-x+\frac{x^2+1}{x-2}) : \frac{3x-1}{x-2$

Înmulțim cu a doua fracție răsturnată.

$\Rightarrow E(x)=(1-x+\frac{x^2+1}{x-2})\cdot \frac{x-2}{3x-1}$

Aducem la același numitor în paranteză.

$\Rightarrow E(x)=(_{{}}^{x-2)}\textrm{1}- _{{}}^{x-2)}\textrm{x}+\frac{x^2+1}{x-2})\cdot \frac{x-2}{3x-1}$ $\Rightarrow E(x)=(\frac{x-2}{x-2}- \frac{x(x-2)}{x-2}+\frac{x^2+1}{x-2})\cdot \frac{x-2}{3x-1}$
$\Rightarrow E(x)=(\frac{x-2-x^2+2x+x^2+1}{x-2})\cdot \frac{x-2}{3x-1}$
$\Rightarrow E(x)=\frac{3x-1}{x-2}\cdot \frac{x-2}{3x-1}$
$\Rightarrow E(x)=1$

Exercițiul 2 (1,5 puncte):

Se consideră funcția $f : R \to R ,$ $f(x)= -x+2$ .

a) Calculați media aritmetică a numerelor $a=f(0)$ și $b=f(2)$ .

b) Reprezentați grafic funcția f(x).

c) Calculați aria triunghiului determinat de graficul funcției f(x) și axele de coordonate OX și OY.

Rezolvare:

a) $f(0)=0+2=2$

$f(2)=-2+2=0$

$M_{a}=\frac{f(0)+f(2)}{{2}} \Rightarrow$ $M_{a}=\frac{2+0}{{2}} \Rightarrow$ $M_{a}=\frac{2}{{2}} \Rightarrow$ $M_{a}= 1$

b) Pentru a reprezenta grafic funcția f(x) facem intersecția cu cele două axe OX și OY
$\cap OX :$ $y=0 \Rightarrow f(x)=0$ $\Rightarrow -x+2=0$ $\Rightarrow -x=-2$ $\Rightarrow x=2$ $\Rightarrow A(2;0)$
$\cap OY:$ $x=0 \Rightarrow f(0)=0+2=2$ $\Rightarrow B(0;2)$

Exercițiul 3 (1,5 puncte):

O piramidă triunghiulară regulată VABC are latura $AB=4\sqrt{6} cm$ și $VO=2\sqrt{6} cm$ , unde O este centrul bazei ABC. Calculați:

a) aria laterală a piramidei;

b) distanța de la O la planul (VBC)

c) distanța de la punctul A la planul (VBC)

d) măsura unghiului format de planele (VBC) și (ABC).

Rezolvare:

Scriem datele problemei și apoi le analizăm:

Realizăm și desenul:

a) Știm formula arie laterale: $A_{l}= \frac{P_{b}\cdot a_{p}}{2}$ .

Pentru a calcula $A_{{l}}$ trebuie să aflăm mai întâi apotema piramidei $a_{{p}}=VM$ .

VABC este piramidă triunghiulară regulată $\Rightarrow \bigtriangleup ABC$ echilateral $\Rightarrow$ AM înălțimea $\bigtriangleup ABC$ $\Rightarrow AM=\frac{l\sqrt{3}}{{2}}$ $\Rightarrow AM=\frac{AB\sqrt{3}}{{2}}$ $\Rightarrow AM=\frac{4\sqrt{6}\cdot \sqrt{3}}{{2}}$ $\Rightarrow AM=\frac{4\sqrt{6\cdot 3}}{{2}}$ $\Rightarrow AM=\frac{4\cdot 3\sqrt{2}}{{2}}$ $\Rightarrow AM=\frac{12\sqrt{2}}{{2}}$ $\Rightarrow AM=6\sqrt{2} cm$

Știm că $OM= \frac{1}{{3}}\cdot AM$ $\Rightarrow OM= \frac{1}{{3}}\cdot 6\sqrt{2} cm$ $\Rightarrow OM= \frac{6\sqrt{2}}{{3}} cm$ $\Rightarrow OM= 2\sqrt{2}} cm$ .

Aplicăm Teorema lui Pitagora în $\bigtriangleup VOM$ pentru a afla apotema VM.

$\bigtriangleup VOM((\widehat{VOM})=90^\circ )$ $\Rightarrow$ T.P $\Rightarrow VM^2=VO^2+OM^2$ $\Rightarrow VM^2= (2\sqrt{6} cm)^2 + (2\sqrt{2} cm)^2$

$\Rightarrow VM^2= 2^2\cdot (\sqrt{6})^2 cm^2 + 2^2\cdot (\sqrt{2})^2 cm^2$

$\Rightarrow VM^2= 4\cdot 6 cm^2 + 4\cdot 2 cm^2$

$\Rightarrow VM^2= 24 cm^2 + 8 cm^2$

$\Rightarrow VM^2= 32 cm^2$ $\Rightarrow VM= \sqrt{32 cm^2}$ $\Rightarrow VM= \sqrt{16 \cdot2} cm$

$\Rightarrow VM= 4\sqrt{2} cm$

Aflăm și perimetrul bazei. Pentru ca $\bigtriangleup ABC$ este echilateral $\Rightarrow P_{b}= 3 \cdot l$ $\Rightarrow P_{b}= 3 \cdot AB$

$\Rightarrow P_{b}= 3 \cdot 4\sqrt{6} cm$ $\Rightarrow P_{b}= 12\sqrt{6} cm$ .

Înlocuim în aria laterală și obținem:

$A_{l}= \frac{P_{b}\cdot a_{p}}{2}$ $\Rightarrow A_{l}= \frac{12\sqrt{6} cm\cdot 4\sqrt{2} cm}{2}$ $\Rightarrow A_{l}= \frac{12 \cdot 4 \sqrt{6\cdot 2} cm^2}{2}$ $\Rightarrow A_{l}= \frac{48 \sqrt{12} cm^2}{2}$ $\Rightarrow A_{l}= \frac{48 \sqrt{4 \cdot 3} cm^2}{2}$ $\Rightarrow A_{l}= \frac{48\cdot 2 \sqrt{ 3} cm^2}{2}$ $\Rightarrow A_{l}= 48\sqrt{ 3} cm^2$

b) $d(O; (VBC))=?$

Știm că AM înălțime în $\bigtriangleup ABC$ $\Rightarrow \left [ AM \right ]\perp \left [ BC \right ]$ și $\left \{ O \right \} \in AM$ $\Rightarrow \left [ OM \right ]\perp \left [ BC \right ]$

$OM=2\sqrt{2}cm$

c) $d(A; (VBC))=?$

Știm că AM înălțime în $\bigtriangleup ABC$ $\Rightarrow \left [ AM \right ]\perp \left [ BC \right ]$

d) $m(\widehat{ (VOM),(ABC)} )$ =?

$\bigtriangleup VOM((\widehat{VOM})=90^\circ )$ : $sin (\widehat{VMO})= \frac{VO}{{VM}}$ $=\frac{2\sqrt{6}cm}{4\sqrt{2}cm}$ $=\frac{\sqrt{3}}{2}$ $\Rightarrow m((\widehat{VMO})= 60^\circ)$ $\Rightarrow m((\widehat{VMA})= 60^\circ)$ .

Dragul meu părinte, sper din tot sufletul ca aceste informaţii să îţi fie utile atunci când îţi ajuţi copilul la temele pentru acasă la matematică. Dacă ai întrebări sau comentarii le poţi lăsa aici în rubrica de comentarii sau îmi poti trimite un e-mail la adresa:nistor_madalina2005@yahoo.com

Dacă ai în jurul tău un parinte sau un copil care are dificultăți în a înțelege matematica fă un gest frumos și recomandă-i

“Math More Easy Club”

Cu mare drag şi mult respect Alina Nistor!

Matematica Mai Usoara

Etichetă: functii

Exerciții Rezolvate la Graficul Funcției

Model Rezolvat Teza clasa a VIII-a Semestrul II

Model Propus Teza clasa a VIII-a Semestrul II